6 Deskriptive Statistik
Deskriptive Statistik wird benutzt, um Daten anhand von Kennzahlen zu beschreiben. Diese Kennzahlen werden auch häufig statistische Maße oder statistische Parameter gennant. Vor allem bei umfangreichen Datensätze können deskriptive Statistiken helfen einen Überblick über die vorhandene Datenstruktur zu gewinnen.
Zu den gängigsten (deskriptiven) statistischen Maßen zählen sogenannten Lagemaße, wie der Mittelwert oder der Median, welche Maße für die zentrale Tendenz einer Häufigkeitsverteilung darstellen (z.B. der Werte in einer Variable).
Andere statistische Maße, wie die Standardabweichung oder die Varianz, erlauben dagegen Aussagen über die Streuung der Werte in einer Variable (sogenannte Streuungsmaße).
Es gibt andere deskriptive Maße, die Aussagen über Zusammenhänge zwischen verschiedener Variablen in einem Datensatz geben (sogenannte Zusammenhangsmaße). Hierzu zählt beispielsweise die Korrelation.
Häufig kommen deskriptive Statistiken im Rahmen von einer Explorativen Datenanalyse (EDA) zum Einsatz. EDA stellt häufig dein Einstieg in einer meistens komplexeren und (häufig) theoriegeleitete Datenanalyse. EDA wird auch häufig dazu verwendet die Qualität und Struktur der Daten zu untersuchen.
In diesem Kapitel berechnen wir verschiedene statistische Maße, um einen Überblick (oder einen ersten Eindruck) der Daten in einem Datensatz zu gewinnen.
6.1 Allgemeine Informationen eines Datensatzes
Für den folgenden Abschnitt benötigen Sie den iris Datensatz. Der iris Datensatz ist
Teil von der Basisinstallation von R und wird automatisch (im Hintergrund) geladen. D.h. Sie
können auf den Datensatz zugreifen in dem Sie iris in die R-Konsole eingeben.
Benutzen Sie head(data), um die ersten 5 Zeilen des Datensatzes zu sehen.
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1 5.1 3.5 1.4 0.2 setosa
## 2 4.9 3.0 1.4 0.2 setosa
## 3 4.7 3.2 1.3 0.2 setosa
## 4 4.6 3.1 1.5 0.2 setosa
## 5 5.0 3.6 1.4 0.2 setosa
## 6 5.4 3.9 1.7 0.4 setosaEine weitere Funktion, mit der Sie die Struktur eines Datensatzes untersuchen können
ist str().str() steht für structure. Der output dieser Funktion zeigt Basisinformationen des
Datensatzes, wie die Anzahl and Beobachtungen (d.h., obs. für observations) und
Variablen (d.h., variables). Wie Sie wissen, stehen Beobachtungen in den Zeilen und Variablen in den
Spalten eines Datensatzes.
## 'data.frame': 150 obs. of 5 variables:
## $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
## $ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
## $ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
## $ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
## $ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...str() erlaubt erste Einblicke in den Datensatz. Oben sehen Sie einige Informationen,
wie beispielsweise Name (z.B., Sepal.Length), Variablen-Typ (z.B., num für numerisch),
sowie typische Werte, die die verschiede Variablen im Datensatz annehmen können
(z.B., 5.1 4.9 4.7 4.6).
Der Datensatz erhält also 150 Beobachtungen und 5 Variablen. Es handelt sich
um die Länge und Breite des Kelch- und des Blütenblattes sowie die Art von 150 Blumen.
Länge und Breite des Kelch- und Blütenblattes sind numerische Variablen.
Die Art der Blume ist ein Faktor mit 3 Stufen (d.h., Factor w/ 3 levels).
6.2 Lagemaße
6.2.1 Minimum und Maximum
Minimum und Maximum können mit den Funktionen min() und max() ermittelt werden:
## [1] 4.3## [1] 4.4Alternativ, können Sie range() (Spannweite) benutzen, um Minima und Maxima zu berechnen:
# Berechnen wir die Spannweite von Sepal.Width und speichern
# wir das Ergebnis in einer neuen Variable namens "width_range"
width_range <- range(data$Sepal.Width)
width_range## [1] 2.0 4.4Wie Sie sehen, berechnet range() einen Vektor, der das Minimum und das
Maximum (in dieser Reihenfolge) enthält.
Genau genommen müssen Sie diese Werte von einander abziehen, um die Spannweite von
Sepal.Width zu bekommen:
## [1] 2.4Die Spannweite beträgt also 2.4. Dies bedeutet, dass der Unterschied zwischen dem breitesten und dem dünsten Kelchblatt 2.4 cm beträgt.
6.2.2 Quantile und Perzentile
Andere häufig eingesetzte deskriptive Parameter sind Quantile oder Perzentile (d.h. welche Werte sind < 25%, < 50%, < 75%, oder > 75%)
Ein häufig verwendetes Perzentil ist der Median. Der Median ist äquivalent zum 50. Perzentil (d.h. 50%) einer Variable, weil 50% der Werte einer Variable unterhalb/oberhalb dieses Wertes liegen.
Der Median kann folgendermaßen berechnet werden:
\[ (1)\qquad \tilde{x}=\left\{\begin{array}{lll} x_{m+1} & \mathrm{für}\; \mathrm{ungerades} \; n &= 2m+1 \\ \frac{1}{2}\left(x_{m}+x_{m+1}\right) & \mathrm{für} \; \mathrm{gerades} \; n &= 2m \end{array}\right. \]
Ein Wert m is Median einer Stichprobe, wenn mindestens die Hälfte der Stichprobenelemente nicht
größer als m und mindestens die Hälfte nicht kleiner als m ist.
Sortiert man die Beobachtungswerte der Größe nach, so entspricht der Median bei einer ungeraden Anzahl von Beobachtungen dem Wert der in der Mitte dieser Folge liegenden Beobachtung. Bei einer geraden Anzahl von Beobachtungen gibt es kein einzelnes mittleres Element, sondern zwei. Der Median entspricht dann (vereinfacht ausgedruckt), dem Mittelwert dieser beiden Beobachtungen.
Sie können diese Annahme mit den Funktionen median() und quantile() überprüfen.
## [1] 5.8## 50%
## 5.8Sie können quantile() auch benutzen, um unterschiedliche Perzentile auf einmal zu berechnen.
# mit 0.25, 0.5, und 0.75 können wir die Grenzen für die
# verschiedenen Quartile berechnen
quantile(data$Sepal.Length, c(0.25, 0.5, 0.75))## 25% 50% 75%
## 5.1 5.8 6.4Dies bedeutet, dass 25% der Werte sich unterhalb von 5.1, 50% unterhalb von 5.8 und 75% unterhalb 6.4 befinden. Im Umkehrschluss befinden sich 25% der Werte oberhalb 6.4.
6.2.3 Interquantilsabstand (IQA)
Manchmal möchte man wissen wie groß der Abstand zwischen bestimmten Quantilen ist, um Aussagen über Beobachtungen, die innerhalb oder außerhalb eines bestimmten Wertebereichs liegen, zu treffen. Häufig wird hierfür der Interquartilsabstand benutzt, welches als der Abstand zwischen den 75. und 25. Perzentil definiert ist.
## [1] 1.3Sie können dies überprüfen, indem Sie den IQA selbt berechnen.
\[ (2)\qquad \mathrm{IQA} = X_{0.75} - X_{0.25} \]
Sie müssen dafür den 3. Quartil (den 75. Perzentil) und den 1. Quartil (den 25. Perzentil) “händisch” berechnen und diese anschließend von einander abziehen.
## [1] 1.3Den IQA kann ebenfalls anhand eines Boxplots dargestellt werden. Unten sehen Sie das 75. Perzentil (nach unten zeigenden Dreieck), den Median (ein X) und den 25. Perzentil (nach oben zeigenden Dreieck) dargestellt. Den grau schattierten Bereich um den Median, zeigt der Wertebereich, in dem sich 50% der Werte einer Verteilung befinden.
# IQA visualisieren anhand eines Box-Plots
# box-plot
boxplot(data$Sepal.Length, ylim = c(3, 10))
# 0.75 Perzentil
points(quantile(data$Sepal.Length, 0.75),
col = 'red', cex = 2, pch = 6, lwd = 2)
# 0.50 Perzentil (Median)
points(quantile(data$Sepal.Length, 0.50),
col = 'black', cex = 2, pch = 4, lwd = 2)
# 0.25 Perzentil
points(quantile(data$Sepal.Length, 0.25),
col = 'blue', cex = 2, pch = 2, lwd = 2)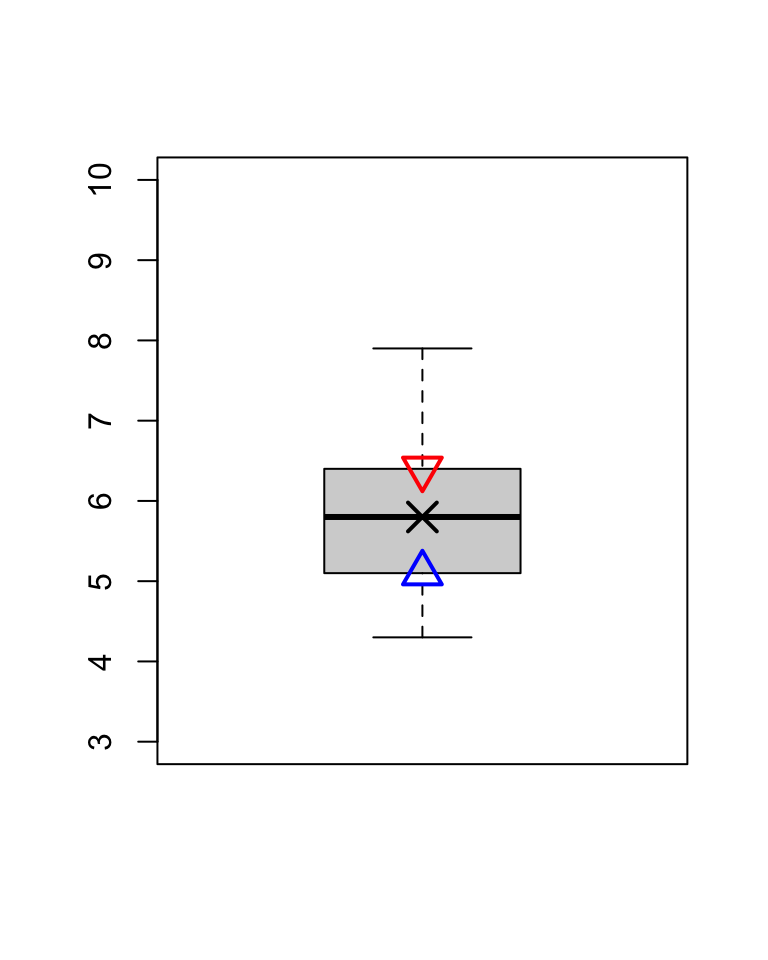
6.2.4 Mittelwert
Ähnlich zum Median, stellt der Mittelwert ein wichtiges Maß für die zentralen Tendenz einer Variable dar. Der Mittlwert (i.S. des arithmetischen Mittels) ist die Summe der gegebenen Werte geteilt durch die Anzahl der Werte.
\[ (3)\qquad \bar{x}=\frac{1}{n}\left(\sum_{i=1}^{n} x_{i}\right)=\frac{x_{1}+x_{2}+\cdots+x_{n}}{n} \] Sie können den Mittelwert also folgendermaßen berechen.
summe_der_werte <- sum(data$Sepal.Width)
anzahl_der_werte <- length(data$Sepal.Width)
# Mittelwert von Sepal.Width
summe_der_werte / anzahl_der_werte## [1] 3.057333Wir können diese Berechnung mit der R-Funktion mean() überprüfen.
## [1] 3.057333Bitte beachten Sie, dass, sollte eine Variable mindestens einen fehlenden Wert erhalten, sollten Sie mean(data$Sepal.Width, na.rm = TRUE), um den Mittelwert unter Ausschluss der fehlenden Werte zu berechnen.
Das Argument na.rm = TRUE kann für die meisten in diesem Abschnitt vorgestellten Funktionen verwendet werden, nicht nur für den Mittelwert.
6.3 Streuungsmaße
6.3.1 Standardabweichung
Die Standardabweichung ist ein Maß für die Breite der Streuung der Werte einer Variable rund um deren Mittelwert (arithmetisches Mittel). Vereinfacht gesagt, ist die Standardabweichung die durchschnittliche Entfernung aller gemessenen Ausprägungen eines Merkmals vom Durchschnitt.
Sie kann folgender Maßen berechnet werden:
\[ (4)\qquad s_{N}=\sqrt{\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}-\bar{x}\right)^{2}} \] In R also:
## [1] 0.4358663Oder mit Hilfe der R-Funktion sd():
## [1] 0.4358663